Cách Tính Diện Tích Mái Thái

Bài viết dưới đây sẽ giới thiệu công thức tính thể tích khối lập phương, công thức tính diện tích hình lập phương, mời các bạn tham khảo.

Diện tích toàn phần khối lập phương

Công thức tính diện tích toàn phần của khối lập phương bằng diện tích một mặt nhân với 6.

Công thức tính bán kính mặt cầu ngoại tiếp khối lập phương

Công thức tính bán kính mặt cầu ngoại tiếp khối lập phương là bán kính mặt cầu ngoại tiếp bằng  độ dài đường chéo của hình lập phương.

Công thức tính diện tích xung quanh của khối lập phương

Bằng diện tích một mặt nhân với 4.

Bài toán về tính diện tích, thể tích khối lập phương

Một hình lập phương A có diện tích toàn phần là 384 cm². Hỏi hình lập phương đó có thể tích bao nhiêu?

Diện tích một mặt của hình lập phương là: 384 : 6 = 64 cm²

Độ dài cạnh của hình lập phương là 8cm do 64 = 8 x 8.

Vậy, thể tích của hình lập phương là 8 x 8 x 8 = 5126 cm³

Diện tích đáy của một bể kính hình hộp chữ nhật là 250cm² và bể đang chứa nước. Biết rằng nếu cho một khối lập phương bằng kim loại cạnh 10cm vào bể (đáy trên khối lập phương bằng mặt nước) thì khối lập phương vừa vặn ngập trong nước . Hãy tính chiều cao mực nước.

Tổng thể tích của lượng nước có trong bể và thể tích khối lập phương là: 250 x 10 = 2500 cm³

Thể tích của khối lập phương là: 10 x 10 x 10 = 1000cm³

Thể tích lượng nước có trong bể là: 2500 – 1000 = 1500cm³

Chiều cao mực nước là: 1500 : 250 = 6cm

Bài 3: Hình lập phương A có cạnh 4 cm. Hình lập phương B có cạnh gấp 2 lần cạnh hình lập phương A. Hỏi thể tích hình lập phương B gấp bao nhiêu lần thể tích hình lập phương A.

Ta có 512 ÷ 64 = 8. Vậy : Thể tích hình lập phương B gấp 8 lần thể tích hình lập phương A.

Công thức tính diện tích xung quanh hình lập phương

Ví dụ: Tính diện tích của một hình lập phương có 6 cạnh đều có kích thước bằng nhau với chiều dài là 4cm.

Gọi a là chiều dài các cạnh của hình lập phương.

Áp dụng theo công thức tính diện tích hình lập phương, ta có:

Bài 4: Người ta làm một cái hộp không có nắp bằng bìa cứng dạng hình lập phương có cạnh 2,5 dm. Tính diện tích phần bìa dùng để làm hộp.

Vì không có nắp nên chỉ có 5 mặt. Vậy diện tích phần bìa dùng để làm hộp là:

Diện tích bìa cần dùng để làm hộp là:

Ví dụ 2: Có hai hình lập phương, diện tích toàn phần của hình lập phương thứ nhất là 486 cm², diện tích toàn phần của hình lập phương thứ hai là 54 cm². Hỏi:

a, Diện tích toàn phần của hình lập phương thứ nhất gấp mấy lần diện tích toàn phần hình lập phương thứ hai?

b, Cạnh của hình lập phương thứ nhất gấp mấy lần cạnh của hình lập phương thứ hai?

a, Diện tích toàn phần của hình lập phương thứ nhất gấp diện tích toàn phần hình lập phương thứ hai số lần là:

b, Diện tích một mặt của hình lập phương thứ nhất là:

Vì 81 = 9 x 9 nên cạnh của hình lập phương thứ nhất là 9cm

Diện tích một mặt của hình lập phương thứ hai là:

Vì 9 = 3 x 3 nên cạnh của hình lập phương thứ nhất là 3cm

Cạnh của hình lập phương thứ nhất gấp cạnh của hình lập phương thứ hai số lần là:

Bài 6: Một căn phòng dạng hình lập phương có độ dài cạnh là 7m. Người ta muốn quét vôi trần nhà và 4 mặt tường của phòng. Trên 4 mặt tường có 2 cửa ra vào mỗi cửa có chiều dài 1,6m và chiều rộng 2,2m và 4 cửa sổ, mỗi cửa có chiều dài 1,2m và rộng 1,5m. Tiền thuê quét vôi 1 mét vuông hết 1500 đồng. Hỏi tiền công quét vôi căn phòng đó hết bao nhiêu?

Diện tích xung quanh của hình lập phương là:

Diện tích một mặt của hình lập phương là:

Diện tích cần sơn (chưa tính các cửa) là:

245 – 3,52 x 2 – 1,8 x 4 = 230,76 (m2)

Mong rằng bài viết này sẽ giúp các bạn biết thêm kiến thức về hình lập phương. Bookmark bài viết và mở ra khi bạn cần nhé.

Ngoài diện tích của hình lập phương, thể tích hình lập phương, các bạn có thể tìm hiểu thêm về các công thức tính diện tích, thể tích của các hình khác như hình vuông, hình bình hành, hình chữ nhật, khối lăng trụ...

Cho em hỏi cách tính điểm trung bình tích lũy ạ. Học kì 1 em có rớt 1 môn, 4đ. Nếu theo số tay sinh viên thì môn đó KHÔNG tính vào điểm TB tích lũy (em sẽ đc 8.44) nhưng khi đọc thông báo kết quả điểm rèn luyện có kèm theo điểm TB thì HK1 em là 7.96 - đồng nghĩa với 4đ rớt môn của em bị tính vào điểm TB. Em xin hỏi tại sao lại như vậy? Và học kì 2 em thi đậu môn đó với số điểm là 5, thì điểm đó tính cho HK2, hay HK1 ạ? Em còn 1 thắc  mắc là học bổng khuyến kích học tập thì lấy điểm trung bình có tính cả điểm của các môn bị rớt không? Và nếu rớt môn mà > số phẩy TB qui định thì có được học bổng không ạ!   Em xin cảm ơn!

Offenbar hast du diese Funktion zu schnell genutzt. Du wurdest vorübergehend von der Nutzung dieser Funktion blockiert.

Wenn dies deiner Meinung nach nicht gegen unsere Gemeinschaftsstandards verstößt,

Chương trình hình học trong bậc trung học phổ thông rất đa dạng về các loại hình và chúng cũng rất dễ dàng gây khó khăn trong việc nhận biết và hiểu rõ về chúng. Đặc biệt là khối lập phương, vậy làm sao để ta có thể phân biệt và làm rõ được các tính chất thì chủ đề này sẽ giúp ta trả lời những thắc mắc đó.

Khối lập phương trong hình học được định nghĩa là 1 khối platon 3 chiều, được tạo thành bởi 12 cạnh bằng nhau, 6 mặt của khối lập phương đều là hình vuông, trong đó có 8 điểm được xem là đỉnh.

Khối lập phương là tập hợp những điểm nằm bên trong và các điểm nằm trên các mặt, cạnh, đỉnh này.

Một khối được xem là khối lập phương nếu nó mang những đặc điểm sau:

• Là hình khối lục diện vuông, hình hộp chữ nhật các cạnh bên luôn bằng nhau, hay hình khối mặt thoi vuông

• Là hình khối mà các mặt bên của nó là sáu hình vuông bằng nhau

• Đường chéo các mặt bên đều dài bằng nhau

• Đường chéo của hình khối cũng dài bằng nhau.

Công thức tính bán kính mặt cầu nội tiếp khối lập phương là bán kính

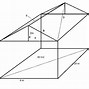
• Bước 1: Vẽ mặt đáy: vẽ hình bình hành ABCD – chính là mặt đáy khối lập phương ABCDEFGH.

• Bước 2: Lần lượt dựng các đường cao có độ dài a, ta được các đường cao AE, BF, CG, DH = a.

• Bước 3: Nối các đỉnh E,F,G,H ta được khối lập phương ABCDEFGH

Lưu ý: Kẻ nét đứt cho AD, DC, HD vì đây là những đoạn bị lấp.

Bài 1: Khối lập phương là khối đa diện đều loại nào sau đây?

Khối đa diện đều thuộc loại {n;p} là khối đa diện đều mà mỗi mặt của đa diện đều là tứ giác đều n cạnh, mỗi đỉnh của đa diện đều là đỉnh chung của p cạnh.

Dựa vào lí thuyết về khối đa diện đều ta có khối lập phương thuộc loại {4;3}

Bài 2: Tính thể tích của khối lập phương có cạnh bằng 4.

Thể tích của hình lập phương có cạnh bằng a là: V = a3

Thể tích của hình lập phương có cạnh bằng 4 là: V = 43 = 64

Bài 3: Tính thể tích V của khối lập phương có các đỉnh là trọng tâm các mặt của khối bát diện đều cạnh a.

Sử dụng công thức tính thể tích hình lập phương cạnh x là

Gọi K là trung điểm AB, M là trung điểm CD.

Ta có khối lập phương cần tìm là QPHJ.Q’P’H’J’.

Xét tam giác SKM có Q là trọng tâm tam giác SAB và H là trọng tâm tam giác SCD.

Mà K là trung điểm A và M là trung điểm CD nên KM = AD = a nên

Xét tam giác QPH vuông cân tại P, theo định lý Py-ta-go ta có

Vậy khối lập phương cần tìm có cạnh nên có thể tích là

Bài 4: Tính thể tích của khối lập phương có cạnh bằng a.

Công thức tính thể tích khối lập phương

Thể tích khối lập phương cạnh a là V = a3

Bài 5: Cho khối lập phương ABCD.A'B'C'D' có O và O' lần lượt là tâm các hình vuông ABCD và A'B'C'D'. Gọi V1 là thể tích khối nón tròn xoay có đỉnh là trung điểm của OO' và đáy là đường tròn ngoại tiếp hình vuông A'B'C'D', V2 là thể tích khối trụ tròn xoay có hai đáy là hai đường tròn nội tiếp hai hình vuông ABCD và A'B'C'D'. Tỷ số thể tích là:

Xác định bán kính đáy là bán kính đường tròn ngoại tiếp hình vuông và chiều cao tương ứng theo dữ kiện của bài toán

Khối nón có chiều cao ,bán kính đáy

Khối trụ có chiều cao ,bán kính đáy

Vậy qua các nội dung chúng ta vừa tìm hiểu về khối lập phương thì để hiểu và làm chính xác những dạng bài tập này, đây là dạng bài tập về hình học sẽ thường xuyên xuất hiện từ 3-4 câu trắc nghiệm trong kỳ thi trung học phổ thông quốc gia theo các mức độ lần lượt từ thông hiểu đến vận dụng cao.

Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang